ファイナンシャル・プランニング（FP)技能検定1級 【基礎編】6つの係数の３つのポイント

ライフプランを作成するときに、資金の積立額や取崩額を試算します。その際に使うのが6つの係数です。

6つの係数は利率一定、期間一定、複利運用を前提として、速算で金額を算出する方法です。

6つの係数は過去12回の試験で3回出題されています。頻出問題ではありませんが、FPには必須事項なのでこの際完璧に理解しておきましょう。

2級、3級を目指す人にも参考になりますよ。

3つのポイント

6つの係数のポイントは以下の3つです。

1番が基本の基本です。
2番は慣れて下さい。慣れてしまえばラッキー問題になります。
3番は1級用です。少し込み入っていますがこれも慣れれば問題ありません。

各種の係数

終価係数と現価係数

終価係数
現在の価格（現価）から将来の価格（終価）を求めるために使います。

現価係数
将来の価格（終価）から現在の価格（現価）を求めるために使います。

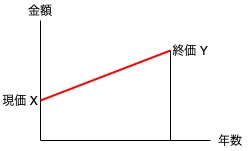
「a ✕ b ＝ 1」は2つの係数が逆数の関係にあることを示しています。

「a ＝ 1／b」に変形して、
終価Y ＝ 現価X ✕ 終価係数a
現価X ＝ 終価X ✕ 現価係数b
に代入すると、

終価Y ＝ 現価X ／ 現価係数b
現価X ＝ 終価Y ／ 終価係数a
が導き出されます。

年金終価係数と減債基金係数

年金終価係数
毎年の積立額（減債基金積立額）から将来の価格（年金終価）を求めるために使う。

減債基金係数
将来の目標価格（年金終価）から、毎年の積立額（減債基金積立額）を求めるために使う。

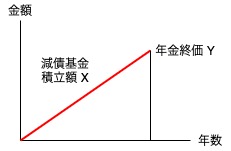
【キーワード】　積立

資本回収係数と年金現価係数

資本回収係数
現在の価格（年金現価）を返却する場合に、毎年の返却額（資本回収額）を求めるために使う。
現在の価格（年金現価）を受け取る場合に、毎年の受取額（資本回収額）を求めるために使う。
現在の価格（年金現価）を取り崩す場合に、毎年の取崩額（資本回収額）を求めるために使う。

年金現価係数
毎年の返却額（資本回収額）から現在必要な価格（年金現価）を求めるために使う。
毎年の受取額（資本回収額）から現在必要な価格（年金現価）を求めるために使う。
毎年の取崩額（資本回収額）から現在必要な価格（年金現価）を求めるために使う。

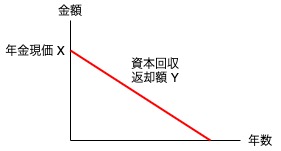
【キーワード】　返却、受取、取崩

理解のポイント

文章を読んでどの係数を使用するのか、理解できること

【問題】

1. 年利3%10年間で100万円を貯めるには、毎年いくら貯金する必要があるか？
2. 年利3％の借入金500万円を10年間毎年返済する場合の年返済額はいくらか？
3. 年利3%10年間で100万円を貯めるには、いくらのお金が必要か？
4. 年利３％で運用している個人年金から10年間毎年20万円を受け取るためには元金はいくら必要か？
5. 年利3％で毎年20万を貯金すると、10年後にいくらになるか？
6. 100万円を年利3%で運用した場合、10年後の金額はいくらか？

期 間	10年
終価係数	1.3439
現価係数	0.7441
減債基金係数	0.0872
年金終価係数	11.4639
資本回収係数	0.1172
年金現価係数	8.5302

【解答】

1
1,000,000円 ✕ 減債基金係数0.0872
＝ 87,200円

2
5,000,000円✕ 資本回収係数0.1172
＝ 586,000円

3
1,000,000円✕ 現価係数0.7441
＝ 744,100円

4
200,000円✕ 年金現価係数8.5302
＝ 1,706,040円

5
200,000円✕ 年金終価係数11.4639
＝ 2,297,780円

6
1,000,000円✕ 終価係数1.3439
＝ 1,343,900円

【解説】

回答のための手順

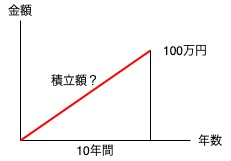
①「毎年いくら」とありますので、年額を算出する問題です。
次に、「10年間で100万円を貯める」とありますので、将来の目標額が100万円とわかります。

次のグラフがイメージできれば減債基金係数を使う問題だとわかります。

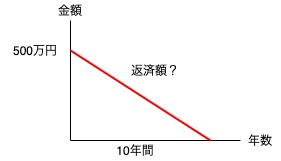
2「年返済額は」とありますので、年額を算出する問題です。
次に、「借入金500万円」とありますので、現在の額が100万円とわかります。

以上から次のグラフがイメージできれば資本回収係数を使う問題だとわかります。

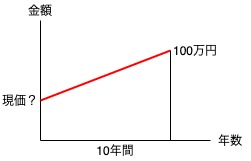
3「いくらのお金が必要か」とありますので、現在の必要額を算出する問題です。
次に、「10年間で100万円を貯める」とありますので、将来の額が100万円とわかります。

以上から次のグラフがイメージできれば現価係数を使う問題だとわかります。

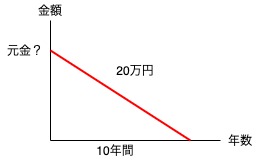
4「元金はいくら必要か」とありますので、現在の必要額を算出する問題です。
次に、「毎年20万円を受け取る」とありますので、受取額が20万円とわかります。

以上から次のグラフがイメージできれば年金現価係数を使う問題だとわかります。

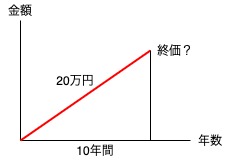
5「10年後にいくらになるか」とありますので、将来の額を算出する問題です。
次に、「毎年20万を貯金する」とありますので、積立額が20万円とわかります。

以上から次のグラフがイメージできれば年金終価係数を使う問題だとわかります。

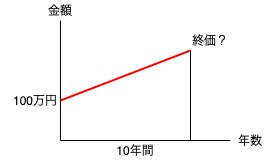
6「10年後にいくらになるか」とありますので、将来の額を算出する問題です。
次に、「100万円を年利3%で運用」とありますので、現在100万円あることがわかります。

以上から次のグラフがイメージできれば終価係数を使う問題だとわかります。

係数が与えられなくても、問題が解けること

先程の問題をもう一度

年利3%10年間で100万円を貯めるには、毎年いくら貯金する必要があるか？

期　間	10年
現価係数	0.7441
年金終価係数	11.4639
年金現価係数	8.5302

減債基金係数の問題ですが、減債基金係数が資料にありません。その場合は、
「減債基金係数 ✕ 年金終価係数 ＝ 1」を変形して
「減債基金係数 ＝ 1 ／ 年金終価係数」を使います。

1,000,000円 ✕ 減債基金係数
＝ 1,000,000円 ✕ 1 ／ 年金終価係数
＝ 1,000,000円 ／ 11.4639
＝ 87,230円
端数の関係で少し違います。誤差です。

複数の係数を使う問題に慣れること

【問題1】
60歳から10年間にわたって、個人年金を毎年70万円を受け取るために、40歳から60歳までの20年間、一定額を毎年積み立てる。この場合の積立額はいくらになるか。
積立、受取とも運用は複利で年2%とする。
円未満は四捨五入すること。

期　間	10年	15年	20年
終価係数	1.219	1.3459	1.4859
現価係数	0.8203	0.743	0.673
減債基金係数	0.0913	0.0578	0.0412
年金終価係数	10.9497	17.2934	24.2974
資本回収係数	0.1113	0.0778	0.0612
年金現価係数	8.9826	12.8493	16.3514

【解答1】
年金現価額
＝ 700,000円 ✕ 10年年金現価係数8.9826
＝ 6,287,820円ｇ

積立額（減債基金額）
＝ 6,287,820円 ✕ 20年減債基金係数0.0412
＝ 259,058円

【解説1】
「毎年の積立額はいくらになるか」とありますので、積立額を算出する問題です。
目標額が問題文からわかりませんが、「10年間にわたって毎年70万円を受け取る」とあることから、受取額が70万円であることがわかります。

以上から次のグラフがイメージできればできれば解答が見えてきます。

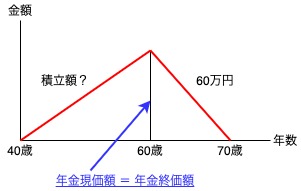
右側の三角形で年金現価額が算出できます。
算出された年金現価額は左側の三角形では年金終価額になります。
年金現価額 ＝ 年金終価額から積立額（減債基金額）を算出します。　

【問題2】
2,000万円を年2％で複利運用しながら15年間、毎年100万円を取り崩した場合、15年後の残額はいくらか。
円未満は四捨五入すること。

期　間	15年
終価係数	1.3459
現価係数	0.743
減債基金係数	0.0578
年金終価係数	17.2934
資本回収係数	0.0778
年金現価係数	12.8493

【解答2】
取崩総額（年金終価）
＝ 1,000,000円 ✕ 年金終価係数17.2934
＝ 17,293,400円

未使用額
＝ 20,000,000円 ー 17,293,400円
＝ 2,706,600円

増加額（終価額）
＝ 2,706,600円 ✕ 終価係数1.3459
＝ 3,642,813円

【解説2】
問題文から下記のグラフが書ければ解答できます。

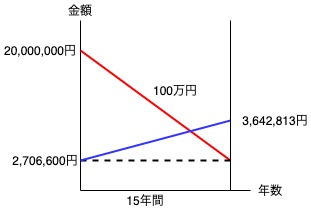
15年間100万円を取崩すので、年金終価係数を使って取崩総額（年金終価）を計算します。
（図の赤線）

2,000万円ー 取崩総額（年金終価）＝ 未使用額になります。
未使用額は利子を生みますので終価係数を使って計算します。
（図の青線）

※ 未使用額が利子を生むことを忘れないように

まとめ

一覧表にまとめるとこんな感じになります。参考まで

	一括タイプ	積立タイプ	取崩(返却)タイプ
将来額	終価係数	年金終価係数	資本回収係数
現在額	現価係数	減債基金係数	年金現価係数